Komponen Teras Panduan Inersia:Giroskop Gentian Optik

Pengenalan kepada Giroskop Gentian Optik

Sistem navigasi inersia sangat bergantung pada ketepatan dan kejituan komponen terasnya. Salah satu komponen yang telah meningkatkan keupayaan sistem ini dengan ketara ialah Giroskop Gentian Optik (FOG). FOG ialah sensor kritikal yang memainkan peranan penting dalam mengukur halaju sudut pembawa dengan ketepatan yang luar biasa.

Operasi Giroskop Gentian Optik

FOG beroperasi berdasarkan prinsip kesan Sagnac, yang melibatkan pemisahan pancaran laser kepada dua laluan berasingan, membolehkannya bergerak dalam arah yang bertentangan di sepanjang gelung gentian optik bergelung. Apabila pembawa, yang terbenam dengan FOG, berputar, perbezaan masa perjalanan antara kedua-dua pancaran adalah berkadar terus dengan halaju sudut putaran pembawa. Kelewatan masa ini, yang dikenali sebagai anjakan fasa Sagnac, kemudiannya diukur dengan tepat, membolehkan FOG memberikan data yang tepat mengenai putaran pembawa.

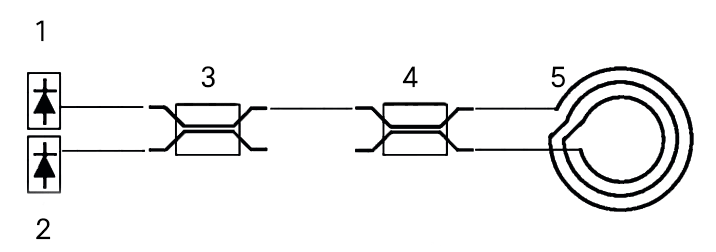
Prinsip giroskop gentian optik melibatkan pemancaran pancaran cahaya dari fotodetektor. Pancaran cahaya ini melalui pengganding, masuk dari satu hujung dan keluar dari hujung yang lain. Ia kemudian bergerak melalui gelung optik. Dua pancaran cahaya, yang datang dari arah yang berbeza, memasuki gelung dan melengkapkan superposisi koheren selepas berputar. Cahaya yang kembali memasuki semula diod pemancar cahaya (LED), yang digunakan untuk mengesan keamatannya. Walaupun prinsip giroskop gentian optik mungkin kelihatan mudah, cabaran yang paling ketara terletak pada menghapuskan faktor yang mempengaruhi panjang laluan optik dua pancaran cahaya. Ini adalah salah satu isu paling kritikal yang dihadapi dalam pembangunan giroskop gentian optik.

1：diod superluminesen           2：diod fotopengesan

3. pengganding sumber cahaya           4.pengganding cincin gentian            5. cincin gentian optik

Kelebihan Giroskop Gentian Optik

FOG menawarkan beberapa kelebihan yang menjadikannya sangat berharga dalam sistem navigasi inersia. Ia terkenal dengan ketepatan, kebolehpercayaan dan ketahanannya yang luar biasa. Tidak seperti giro mekanikal, FOG tidak mempunyai bahagian yang bergerak, sekali gus mengurangkan risiko haus dan lusuh. Selain itu, ia tahan terhadap kejutan dan getaran, menjadikannya sesuai untuk persekitaran yang mencabar seperti aplikasi aeroangkasa dan pertahanan.

Integrasi Giroskop Gentian Optik dalam Navigasi Inersia

Sistem navigasi inersia semakin menggabungkan FOG kerana ketepatan dan kebolehpercayaannya yang tinggi. Giroskop ini menyediakan ukuran halaju sudut penting yang diperlukan untuk penentuan orientasi dan kedudukan yang tepat. Dengan mengintegrasikan FOG ke dalam sistem navigasi inersia sedia ada, pengendali boleh mendapat manfaat daripada ketepatan navigasi yang dipertingkatkan, terutamanya dalam situasi di mana ketepatan yang melampau diperlukan.

Aplikasi Giroskop Gentian Optik dalam Navigasi Inersia

Kemasukan FOG telah memperluaskan aplikasi sistem navigasi inersia merentasi pelbagai domain. Dalam aeroangkasa dan penerbangan, sistem yang dilengkapi FOG menawarkan penyelesaian navigasi yang tepat untuk pesawat, dron dan kapal angkasa. Ia juga digunakan secara meluas dalam navigasi maritim, tinjauan geologi dan robotik canggih, membolehkan sistem ini beroperasi dengan prestasi dan kebolehpercayaan yang dipertingkatkan.

Varian Struktur Giroskop Gentian Optik yang Berbeza

Giroskop gentian optik terdapat dalam pelbagai konfigurasi struktur, dengan yang utama yang sedang memasuki bidang kejuruteraan ialahgiroskop gentian optik pengekalan polarisasi gelung tertutup. Teras giroskop ini ialahgelung gentian pengekalan polarisasi, yang terdiri daripada gentian pengekal polarisasi dan rangka kerja yang direka bentuk dengan tepat. Pembinaan gelung ini melibatkan kaedah penggulungan simetri empat kali ganda, ditambah dengan gel pengedap unik untuk membentuk gegelung gelung gentian keadaan pepejal.